Si te asomas a la ventana seguro que ves un fractal: las nubes, los árboles, las montañas son ejemplos clásicos de este tipo de objetos. También están dentro de nuestro cuerpo: la porosidad de los huesos, los sistemas circulatorio y respiratorio, las neuronas…
Para que un objeto se denomine fractal debe tener al menos dos características: autosimilitud y dimensión fractal.
La autosimilitud se refiere como «la parte es igual al todo», lo cual no siempre es posible en los objetos reales en toda la magnitud de la frase pero si en los rasgos generales. Así podemos entender que las ramas del árbol se parecen al árbol completo.
En la figura de abajo se tiene el triángulo de Sierpinski y se nota como se puede hacer zoom infinidad de veces y seguir viendo lo mismo.

La dimensión fractal indica la complejidad de un objeto respecto a las dimensiones comunes: si el punto tiene dimensión cero, la línea dimensíon 1, el plano dimensión 2 y el cubo dimensión 3, ¿que dimensión se asigna a algo que no es totalmente plano ni totalmente un volumen? La dimensión de un arbol estará entre 2 y 3.
La dimensión fractal del triángulo de Sierpinski es de 1.5850.
La palabrar fractal proviene del latín fractus. Ésta disciplina fué bautizada y formalizada por Benoit Mandelbrot en los setentas.

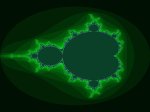
El conjunto de Mandelbrot es el objeto matemático mas complejo.
Agregamos aquí distintas vistas del mismo:
Te recomiendo leer:
Cerramos con un video
Actualizado 12 de octubre de 2012