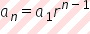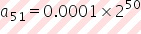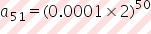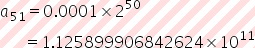Bueno, en la novela Inferno, de Dan Brown.
Tal vez lo que haya que reconocerle a Dan Brown es el uso de elementos matemáticos y científicos para definir las tramas en su novelas: la sucesión de fibonacci y la razon dorada en el codigo, ambigramas y antomateris en Ángeles y Demonios, la susesiones geométricas en Inferno, por citar algunos de las novelas que recuerdo haberle leído.
Sin embargo en este caso, la progresión geométrica solo es mencionada, no se describe su formulación, tal vez para no asustar a los lectores.
De hecho Stephen Hawking meciona otra sucesion para este oficio de los escritos de divulgacion:
«…divide por dos la cantidad de lectores por cada fórmula que pongas en tu texto.»
Brown no pone fórmula alguna pero describe una progresión geométrica:
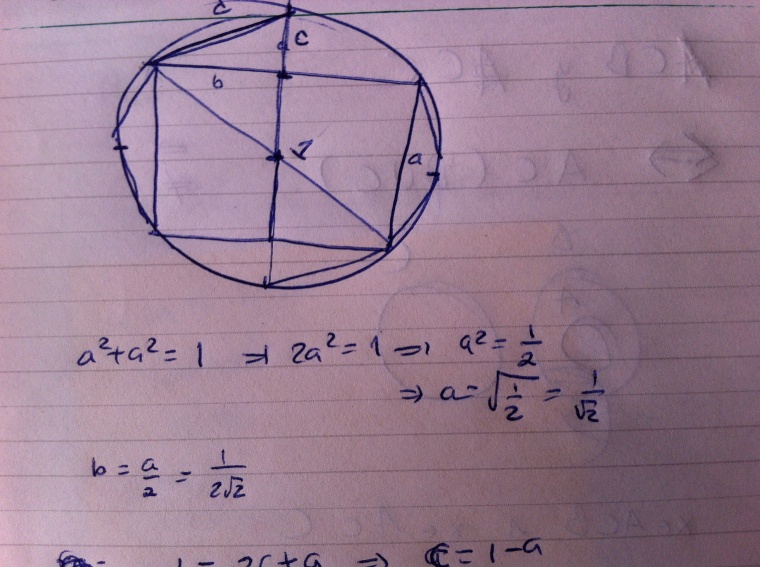
«—Si rompo por la mitad una hoja de papel… —se detuvo junto a la mesa, agarró una hoja de papel y la rasgó—, y luego coloco las dos mitades juntas y repito el proceso… —Volvió a romper los papeles y a juntar sus mitades—, obtendré una pila de papel cuatro veces más gruesa que la original, ¿verdad? —En la oscuridad de la habitación, parecía que sus ojos relucían.
A Elizabeth le molestó su tono condescendiente, y también su actitud hostil. No dijo nada.
—Hablando hipotéticamente —prosiguió él, acercándose a la doctora todavía más—, si el grosor de la hoja de papel original no fuera más que de una décima de milímetro y repitiera el proceso, digamos, cincuenta veces, ¿sabe qué altura alcanzaría la pila?
Elizabeth se sentía indignada.
—Lo sé —respondió con más hostilidad de la que pretendía—. Sería una décima de milímetro multiplicada por dos y elevada a la quincuagésima potencia. A eso se le llama progresión geométrica.»
En este blog haremos las cuentas para verificar el texto anterior.
Para definir una progresión geométrica necesitamos el elemento inicial, a1, y r es la razón por la que se multiplica, en este caso por dos. Así el n-ésimo elemento estará dado por:
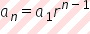
En nuestro caso a1 es una décima de milímetro, que convertido a metros es 0.0001 m, por lo que el término 51 es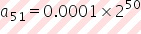 
Lo cual difiere de lo que expresa el párrafo, que en números sería: 
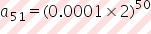«¿Y a quién le importa un paréntesis más o uno menos?», casi le oigo decir eso a un Pibicho.
Bueno, si hacemos la cuenta de la cita tendremos que
Es decir, después del punto decimal tenemos 184 ceros antes de tener la primera cifra significativa. Lo cual significa que es un número muy, pero muy pequeño, que no serviría para asustar en esta novela. Pero si está de acuerdo con la cita de Hawkin, pues cada vez que escribes una fórmula el número de lectores se reduce, y aunque la cifra sea ridícula, en teoría no es cero.
Así que es posible que la traducción haya estado equivocada y en realidad quería decir «una décima de milímetro multiplicada por dos a la la quincuagésima potencia. Con lo cual, usando nuestra primera fórmula tendríamos
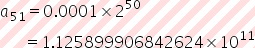
en metros.
Ambos resultados los he calculado en Wolfram Alpha, y ahí nos ayudan a entender este número por medio de comparaciones:
- El número de estrellas que hay en nuestra galaxia es 0.30 por diez a la 11, es decir, es menor que nuestro resultado.
- El número de personas que hayan vivido en toda la historia de la tierra: 1.1 por diez a la 11, un poco menor que este número.
Ese número si asusta, sobre todo si estás hablando de un peligro como el que se describe en la novela.
Por cierto, ¿ya la leíste?
Esta es una entrada hermana de la que está en mi otro blog, no olvides visitarla.
Pi-bichos 